АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОД

В графском парке

• Все журналы \ Номер 33/256 `2003 от 25.08.2003 \ В графском парке

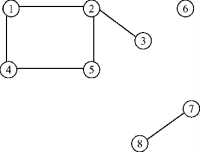
Юрий ДОВГАНЬ freeyuran@ukrpost.net

Вычислительная математика и ряд других наук уже успели «положить глаз» на теорию графов, найдя им применение во многих сферах современной жизни. Впервые о графах заговорил известный математик Леонард Эйлер, который, однажды прогуливаясь, решил составить схему парка и решать разного вида задачки с ее помощью. Сегодня же, мягко говоря, без графов сложно было бы обойтись при решении разного рода экономических, технических, научных вопросов. Что такое графы, как с ними работать и что с их помощью можно осуществить?

Основные понятия

Давайте разберемся с основными терминами теории графов. Графом G является пара множеств G=(V,U), где V — множество (совокупность) вершин, U — множество ребер, соединяющих пары вершин. Разумеется, множества V и U являются конечными: мы можем перечислить все вершины и ребра графа: V={v1, v2, v3,…, vN}, U={u1, u2, u3,…, uM}. Числа N и M являются, соответственно, мощностями множеств V и U, то есть количеством вершин множества V и количеством ребер множества U. Вершинами могут служить объекты любой природы: будь то населенные пункты, компьютеры сети, элементы блок-схем алгоритмов и т.д. Под ребрами, как вы уже догадались, могут подразумеваться дороги между двумя соседними городами, стороны геометрических фигур, связи между компьютерами. Любую систему улиц в городе можно представить в виде графа. Здесь вершины выступают в роли перекрестков. Таким образом, каждое ребро представляет собой пару вершин: начало и конец ребра. Например, если существует ребро uk, началом которого является вершина vs, а концом — вершина vt, то ребро uk можно записать как пару [vs, vt]. Две вершины vs и vt называются смежными в графе, если в нем существует ребро [vs, vt]. Ребро и любая из его двух вершин называются инцидентными. Под степенью вершины подразумевается количество инцидентных ей ребер.

Маршрут (путь) — это последовательность ребер, начало каждого из которых (начиная со второго) совпадает с концом предыдущего. Маршрут является замкнутым (циклом), если его начальная и конечная вершины совпадают. Следовательно, каждый маршрут можно представить как последовательностью ребер, так и последовательностью вершин. Под длиной пути имеется в виду количество ребер в пути, или же количество вершин минус 1. Позже мы столкнемся с таким вопросом как длина ребра во взвешенном графе — в таком случае длина маршрута будет не столь однозначна. Интуитивно понятно, что вершина vs достижима из вершины vt, если между ними проложен маршрут. Идем вглубь. А могут ли в графе содержаться недостижимые вершины? Этот вопрос и приводит к понятию связности графа. Граф считается связным, если все его вершины достижимы из любой другой. Граф называется ацикличным, если он не содержит циклов. И наконец, изолированные вершины. Это такие вершины, которые не имеют инцидентных ребер. Можно также сказать, что их степень нулевая. Из всего этого следует, что изолированные вершины недостижимы из любых других вершин.

Сообразительный читатель может задать вопрос: имеет ли значение направление, ориентация ребра? Ведь в системе улиц можно найти как дороги с односторонним, так и с двусторонним движением. Именно поэтому в теории графов вводится понятие орграфа — ориентированого графа, в котором каждое ребро имеет одно направление. Такие ребра называются дугами. Другими словами, ребро — это неупорядоченная пара вершин, а дуга — упорядоченная. Очевидным является тот факт, что дуги (vs, vt) и (vt, vs) не совпадают в орграфе. Для орграфа вводятся такие понятия как входящая и исходящая степени вершины. Если в первом случае подразумеваются число входящих в вершину дуг, то во втором — число исходящих из нее. Заметим, что в орграфе могут быть и дуги, имеющие оба направления.

Чтобы прояснить сложившуюся ситуацию, вникнуть в смысл всех вышеописанных терминов, давайте разберем наглядный пример графа и опишем все его элементы и свойства.

Опишем множества V и U графа A (Рис. 1.). V(A)={1, 2, 3, 4, 5, 6, 7, 8}, U(A)={[1,2], [1,4], [2,3], [2,5], [4,5], [7,8]}. Поскольку граф A является неориентированным, то любое его ребро может быть записано неупорядоченной парой вершин. Так, ребро [1,4] совпадает с [4,1]. Мощности множеств V и U равняются: |V|=8, |U|=6.

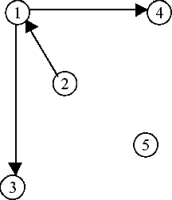
Найдем смежные вершины. Например, для вершины 1 смежными будут 2 и 4, для вершины 4 —1 и 5, для вершины 8 —7, у вершины 6 смежных нету. Ребро [1,2] инцидентно вершинам 1 и 2, вершине 2 инцидентны ребра [1,2], [2,5] и [2,3]. Понятно, что вершина 6 — изолированна и недостижима из любых вершин графа, вершины 8 и 7 недостижимы из вершин 1, 2, 3, 4, 5, 6. Степень вершины 2: St(2)=3; вершины 8: St(8)=1; вершины 6: St(6)=0. Рассмотрим путь [1, 4, 5, 2, 1] (на рисунке выглядит как прямоугольник) — он будет циклом. Его длина равна 4 (количество ребер или количество вершин минус 1). Зато пути [8,7], [1, 4, 5, 2, 3] циклов не образуют. Маршрута [8, 7, 5] не существует, так как вершина 5 недостижима из вершины 7. Соответственно, граф A не является связным, поскольку не всякая его вершина достижима из другой (например, из 6).

Рассмотрим граф B(Рис. 2.) и его свойства. V(B)={1, 2, 3, 4, 5}, U(B)={(1,3), (1,4), (2,1)}. Граф ориентированный: существует дуга (1,3), но не существует (3,1). Свойства смежности, инцидентности рассматриваются подобно предыдущему случаю. С маршрутами дело обстоит по-иному. Существует маршрут [2, 1, 4], но не существует маршрута [3, 1, 4]. На рисунке видно, что вершины 1, 2, 4, 5 недостижимы из вершины 3. Граф B циклов не содержит. Входящая степень вершины 1 равна Stv(1)=1, исходящая —Sti(1)=2.

Взвешенные графы

Выше мы познакомились со структурами, которым присущи те или иные свойства графа. Немного расширяя терминологию теории графов, математика вводит понятие взвешенного графа, или более общо — сети. Сеть — это граф, элементам которого поставлены в соответствие некоторые параметры. Под элементами здесь подразумеваются вершины, дуги (ребра) и образующиеся из них конструкции. Параметры могут быть разными: вес, длина ребра, стоимость (стоимость перевозки из одного пункта в другой), пропускная способность (какой объем товара можно перевезти по ребру) и т.п. Именно взвешенные графы находят применение в жизни. Нахождение кратчайших маршрутов, максимальных потоков, оптимизация на сетях — все эти задачи требуют реализации специальных алгоритмов, построенных на доказанных методах эффективного решения различных задач вычислительной математики, в том числе оптимизационного характера. Но, прежде всего давайте выясним, как описать граф или сеть в памяти компьютера.

Машинное представление графов

Практика показывает, что способ описания графа, то есть выбор соответствующей структуры данных в системе программирования, играет немаловажную роль при разработке эффективных алгоритмов. Для одних алгоритмов выгодно использовать массивы, для других —динамические структуры. К таким типам данных относятся: матрицы смежностей и инцидентностей, списки ребер, списки смежностей и т.п. Будем описывать типы данных с помощью языка Паскаль, ориентируясь на основную массу читателей.

Матрица смежностей — это двухмерный массив размера N*N, где N — количество вершин графа:

Type MatrixOfAdjacencies=array[1..N,1..N] of integer; {тип ячеек может быть не только целочисленным: иногда вершины именуются буквами, словами и т.п.} Var G:MatrixOfAdjacencies; {переменная G объявляется переменной типа "матрица смежностей", таким образом представляя граф G}

Ячейки массива заполняются по правилу:

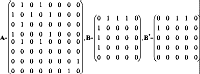
Во взвешенном графе вместо 1 указывается вес (длина) ребра [i,j], стало быть вместо 0 — какое-то отрицательное число (так как вес ребра может принимать нулевое значение). Если учесть ориентацию графа, то можно слегка видоизменить матрицу смежностей, элементы которой будут определяться по правилу:

G*[i,j]=0

если нету дуги (i,j), или

i=j

и

G*[i,j]=1

(весу дуги), если таковая дуга имеется.

Следует напомнить, что в дуге (i,j) вершины i и j будут смежными независимо от направления дуги. В таком случае матрицы смежностей всегда будут симметричны относительно главной диагонали, в то время как матрица G* — нет.

Если обратится к вышеупомянутым примерам графов A и B, то их матрицы смежностей примут следущий вид:

Легко заметить, что матрицы A и B симметричны относительно главной диагонали, а B* — нет, что и требовалось доказать :-).

Примечания. В некоторых источниках матрицу G* могут называть матрицей инцидентностей. На самом деле это не совсем так, исходя даже из определения инцидентности ребра и любой из его двух вершин. Как видим, строчки и столбики матрицы G* имеют индексы вершин графа, в то время как в матрице инцидентностей столбикам отвечают ребра (дуги).

Способ представления графа матрицей смежностей позволяет за одну операцию найти смежную вершину с данной, указать вес ребра; за T(N) (временная сложность алгоритма) операций перечислить все вершины, смежные с заданной; за T(N2) операций перечислить все ребра графа.

Матрица инцидентностей представляет собой двумерный массив размера N*M, где N — количество вершин, M — количество ребер графа.

Type MatrixOfIncidences=array[1..N,1..M] of integer; Var G:MatrixOfIncidences;

При этом

Аналогично с матрицей смежностей в случае со взвешенным графом вместо 1 ставится вес ребра (дуги).

При представлении графа матрицей инцидентностей расход операций на некоторые действия таков:

1. На проверку смежности двух вершин уходит до T(M*N) операций.

2. На определения веса ребер — T(M*N) операций.

3. На перечисление всех вершин, смежных с данной, — T(M*N) операций.

4. Перечисление всех ребер, инцидентных данной вершине, — T(M) операций.

5. Перечисление вершин, инцидентных данному ребру, — T(N) операций.

6. Перечисление всех ребер — T(M) операций.

Список ребер — довольно удобный способ представления графов. Он может представлять собой как динамическую структуру данных (линейный односвязный список), так и массив записей.

Начнем со второго. Опишем тип ListOfRibs:

Type ListOfRibs=array[1..M] of record {массив записей} n1, n2: integer; {начало и конец ребра, соответственно, начальная и конечная вершины} w:integer; {вес (длина, пропускная способность) ребра, если подразумевается сеть} end; Var G: ListOfRibs;

Как это выглядит на деле? А приблизительно так:

Что касается временных затрат:

1. Проверка смежностей двух заданных вершин — T(M) операций.

2. Перечисление всех вершин, смежных с данной, — T(M) операций.

3. Перечислений всех вершин, инцидентных заданному ребру, — T(1) операция.

4. Определение веса ребра (дуги), — T(M) операций.

5. Перечисление ребер, инцидентных заданной вершине, — T(M) операций.

6. Перечисление всех ребер — T(M) операций.

Наверное, каждый программист, знакомый с динамическими списками, может перечислить все их основные преимущества перед массивами. Во многих случаях, действительно, намного удобнее и эффективнее использовать именно линейные односвязные списки. В данном случае списки ребер.

Type ListOfRibsPTR=^GraphList; GraphList=record n1, n2: integer; w: integer; link: ListOfRibsPTR; end; Var G: ListOfRibsPTR; {Указатель на голову списка ребер}

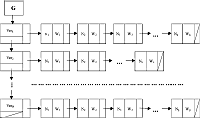
Список смежностей — вот до чего додумались люди! Может быть также двух типов: массив массивов записей (я сам хоть понял, что сказал? :-)) и динамическая структура — список списков.

Начнем с первого. Массив массивов записей — штука довольно-таки сложная и громоздкая, но местами весьма полезная. Итак, приступим.

Type ListOfAdjacencies=array [1..N] of record {массив массивов} Count: integer; {количество вершин, смежных с текущей} List: array[1..N] of record {в каждой ячейке внешнего массива (индекс ячейки соответствует номеру вершины) содержится List — массив смежных с данной} n: integer; {i-я смежная вершина с текущей из внешнего массива} w: integer; {вес ребра} end; end; Var G: ListOfAdjacencies;

Не так сложно описать тип данных, как изобразить это в виде иллюстрации:

Разумеется, здесь k<N, s<N, …, p<N, так как у одной вершины не может быть больше N-1 смежных. Получается, что массивы G[i].List (i=1, 2, 3, …, N) смежных вершин не будут полностью заполнены. В роли счетчика количества вершин в массиве смежных выступает число G[i].Count. Я для удобства не стал помещать на рисунке веса ребер. Они должны располагаться в ячейках наряду с n[j] в виде записей.

Если до сих пор непонятно, как эта штуковина работает, в качестве примера предлагаю простую процедуру, совершающую перечисление всех вершин графа, заданного списком смежности, и перечисление смежных с ними вершин.

Procedure Simple (G: ListOfAdjacencies); Var i,j:integer; BEGIN For i:=1 to N do begin {i — номер текущей вершины} Write('Рассматривается вершина', i, 'имеющая', G[i].Count,'смежных с нею'); For j:=1 to G[i].Count do begin {проходим все смежные вершины} Write('Вершина',G[i].List[j].n, 'смежна с текущей вершиной ', i,'При этом вес ребра =', G[i].List[j].w); {здесь имеется в виду вес ребра [i, G[i].List[j].n]} end;{j} end; {i} END;

Список смежностей в виде массива массивов записей позволяет реализовывать следующие действия с такими временными затратами:

1. Проверка смежности двух вершин — T(N) операций.

2. Перечисление все вершин, смежных с данной — T(N) операций.

3. Перечисление всех ребер — T(M) операций.

4. Определение веса ребра — T(N) операций.

Многим этих способов хватит с головой, но найдутся и такие извращенно-утонченные читатели, которые захотят почувствовать особые изобретательские прелести предыдущих поколений :-). Для самых смелых и отчаянных готов предложить список смежностей в виде динамической структуры — списка списков.

Type LocalList=^LocList; {для каждой вершины из общего списка есть список смежных с нею} LocList=record N: integer; {Номер одной из смежных вершин с текущей} W: integer; {Вес ребра: начало в вершине общего списка, конец — списка смежностей} Link: LocalList; {Указатель на следующую смежную вершину} End; Type MainList=^MaList; {Общий (вертикальный на рисунке) список вершин графа} MaList=record Ver: integer; {Номер вершины} Adj: LocalList; {Указатель на список смежностей для текущей вершины Ver} Next: MainList; {Указатель на следующую вершину графа} End; Var G: MainList; {Переменная G является указателем на голову списка смежностей}

Здесь k<N, s<N, …, p<N.

Разумеется, для разных вершин Veri и Verj (ij) Nt для Veri и Nt для Verj не совпадают. В общем случае это разные вершины. Аналогично, вес Wj ребра [Veri, Nj] не совпадает с весом Wj ребра [Vert, Nj], так как это могут быть разные ребра (хотя индексы у обоих W одинаковые).

На этой радостной и обнадеживающей ноте :-) мы закачиваем сегодняшнюю статью. На очереди — разные алгоритмы на графах.

(Продолжение следует)